Conic Ambiguity Model

Introduction

As explained on the Understanding Ambiguity Codes page, libSlice provides mulitple consensus calling algorithms to choose from. The default consensus calling algorithm uses the "Conic Ambiguity Model", which uses the cumulative quality values to compute a consensus. It was created to address the limitation of the other models and to call the consensus of slices consistently with an expert panel.

Conic Ambiguity Model

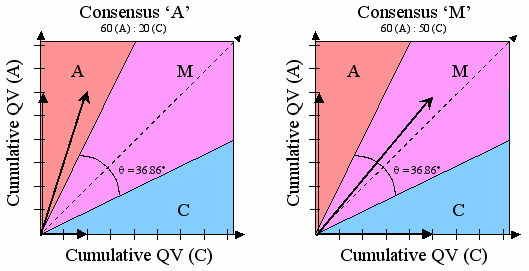
The Conic model compares the ratio of cumulative quality value (cqv) of the five components for a given slice, i.e. if the slice is (A,30), (A,30), and (C,20), A has 60 cqv points, C has 20 cqv points, and G, T, and gap have 0. If the ratio of the top two is near 1:1 (perfect ambiguity), the consensus is ambiguous and marked with the appropriate ambiguity code. If the slice has a ratio that exceeds 2:1, the consensus is called without an ambiguity code as the component with the largest cqv.

The component with the largest cqv is also called the non-ambiguous consensus of the slice. In this example, the ratio is 60:20, or 3:1 between A and C, so the consensus is A, as is the non-ambiguious consensus. If the ratio had been 60:50, the consensus would be M. If there are more than two components with non-zero cqv, then the algorithm iterates in order of cqv expanding the ambiguity code to include each component that is within the 2:1 cutoff in comparison to the non-ambiguous consensus.

The advantage of the Conic model is that it directly addresses the limitations of the other models in that it is sensitive to both the quality values of the slice, and the depth of coverage. High quality agreement is rewarded more strongly than low quality agreement, and many low quality disagreeing bases can balance a few high quality agreements. In our testing, we have found that it significantly outperforms the other models by calling the consensus in agreement with an expert panel for a much higher percentage of slices.

The model is called "Conic" because under a geometric interpretation, a multidimensional cone defines the region of ambiguity. In this interpretation, the cqv of each component is represented by perpendicular vectors. A vector sum is then performed, and if the resultant vector falls within the region of ambiguity, the consensus is ambiguous. From symmetry, the region of ambiguity is defined uniformly from perfect ambiguity by a parameterized angle, which when rotated in a higher dimensional space defines a cone.

At 0 degrees, only perfectly ambiguous slices would be called with an ambiguity code; at 45 degrees all slices are ambiguous. A large effort of the algorithm tuning was to find the angle that maximizes agreement with expert consensus callers. The angle that maximizes the agreement (36.86 degrees) was found to coincidentally define a region where the ratio of cumulative quality values is 2:1. For the common case of only two components present in a slice, the model defines the region of ambiguity as being a triangular zone near 45 degrees.

Conic Ambiguity Calculation

Validation

The conic ambiguity model was validated by comparing the results of its consensus calling to the consensus calling of a panel of experts, made of two PIs and two Closure Specialists. The validation was performed on a set of 100 slices that covered every permutation of high and low quality disagreements up to a 7x depth of coverage, with additional slices up to a 32x depth of coverage. For slices where the experts disagreed, the expert consensus was the base or code that the majority of the experts favored with ties going towards the ambiguity codes.

The Conic model outperformed the other ambiguity models by 20%. It consistently agreed with the expert panel in nearly every slice. The 6 slices that it did not agree with the experts were extreme borderline cases, and were evenly split between calling too many ambiguity codes and too few. In no cases did the Conic model call one unambiguous base where the experts decided the other unambiguous base should be the consensus in the conflicting slices. The Consensus Calling Worksheet of 100 slices used for validation is available, as are the results. It is also worth pointing out that the worksheet slices were directed towards borderline cases because all of the models handle the majority of slices where a single component dominates the slice correctly.

Results

The default ambiguity model in now the Conic ambiguity model because it calls a vastly improved and more useful consensus than the other models. This means the consensus displayed in Cloe, for example, has been called according to the Conic Model. We are investigating the best method for recalling the consensus for projects that are currently in closure or beyond.

$Date: 2005/07/29 02:55:17 $